幂律分布——自然界的另一种数学规律

正态分布几乎每个人都习以为常，它描述的是这样一种数学关系，即一个随机变量的取值在其均值附近的概率较大，而在其均值远处的概率较小。正态分布的概率密度函数呈现出一种优美的钟形曲线，它的形状由两个参数决定：均值和标准差。均值决定了曲线的中心位置，标准差决定了曲线的宽度。

正态分布在自然界和社会现象中有着广泛的应用，例如人类的身高、体重、智商等都可以近似地看作是服从正态分布的。

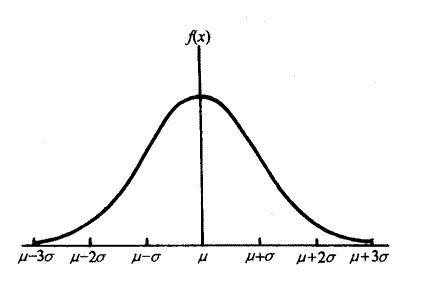正态分布是我们熟悉的数学规律

而幂定律则是自然界另一种常见的数学关系，它描述的是一个量随另一个量的幂而变化的函数关系，而与这些量的初始大小无关。幂定律表现出一种标度不变性的特征，即系统中个体的尺度相差悬殊，缺乏一个优选的规模。

幂定律分布在物理学、地理学、生物学、社会学、经济学等众多领域中都有着广泛的应用，例如地震规模、月坑直径、城市人口、个人收入、单词频率、网页点击率等都是典型的幂定律分布。在此我将介绍几个详细的例子来介绍幂定律分布。

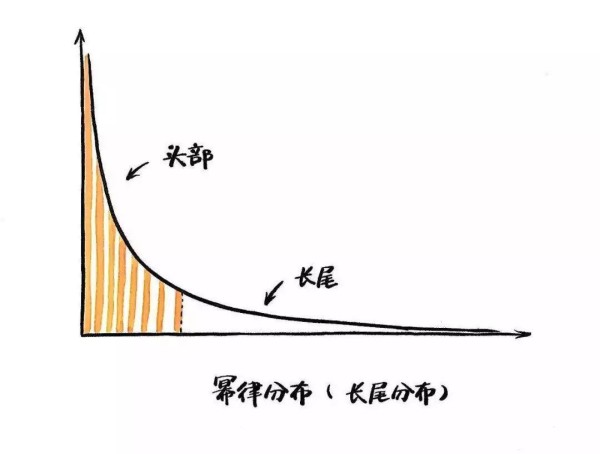幂定律分布也是自然界中常见的数学规律

地震规模

古登堡-里赫特定律是地震学中的一个定律，表示震级与某一地区大于等于该震级的地震数量之间的关系，由地震学家宾诺·古登堡（Beno Gutenberg）和查尔斯·弗朗西斯·里赫特（Charles Francis Richter）于1956年提出。该定律的表达式为：

log10N=a−bM

其中，N表示震级大于等于M的地震数量，a和b是常数，通常b的值在0.8到1.2之间。这个公式说明，随着震级的增加，地震的频率呈指数下降。例如，如果b=1，那么8级地震的概率是7级地震的十分之一，6级地震的百分之一，5级地震的千分之一，以此类推。也就是说，每增加一级震级，地震的概率就减少十倍。

地震每增加一级，概率就减少十倍

生物灭绝

现在存在于地球上的物种只占所有在地球上存在过的物种数量的0.02%不到，绝大多数都在生物演化的过程中灭绝了。谈到灭绝，很容易让人想起五次生物大灭绝。但是，并非所有灭绝都是大规模生物灭绝。演化生物学专家估计，生物历史中曾出现过约10亿种生物。而只有几千万种存留至今。灭绝是演化史的自然结果，正如有些人曾说:“粗略算来，所有生物都灭绝了。”但事实上，只有35%的生物死于集群灭绝。不起眼的“背景”灭绝则造成了约2/3的生物灭绝。

事实上，生物灭绝的规律完全等同于地震规律:若灭绝规模增加1倍，其发生频率便会降为1/4。这种幂定律对于从只涉及几科的小型灭绝到上千科的大灭绝均适用。

生物灭绝规模每增加1倍，频率便降低1/4

战争规模

战争规模，也可以用幂律分布来描述。根据历史数据，从公元前1500年到2003年，发生在世界各地的338次冲突（或战争）的死亡人数可以用幂律分布来拟合。这意味着，大多数战争的规模都很小，只有少数战争的规模非常大。例如，一次战争造成的死亡人数达到或超过一战（约2000万人）的概率为1.1%，而达到或超过二战（约6000万人）的概率为0.3%。

城市规模和人口聚集规模

社会科学家研究美国前2400座大城市的数据，统计拥有10万、20万、30万直至900万人口的城市数目，最后一类中只有纽约市。也就是说，他们采用古登堡和里克特研究地震的方式来研究城市，并发现了类似规律。数据表明，对于每一座规模如亚特兰大的城市——400万人口，对应有4座城市拥有约一半的人口。辛辛那提就是这样的城市，而与它对应的拥有一半人口的城市也是4个，以此类推。这个完美的几何规律一直持续到只有1万人的小城市。因此,尽管所有城市有千万种成因和相互竞争的影响因素，它们都符合一个简单的数学规律。

这种简单性影响可以继续扩展，因为人们在某特定城市中的居住分布也存在特定规律。伦敦或柏林的深夜卫星照片展示出极为不同的图景，也就是说，它们的精确细节迥然各异。但是，只要近距离观察，这些照片呈现的却是同类型的分形图案。任何城市当中都散落着更大或更小的人口聚居地，这样的聚居地符合幂定律。因此，没有典型的群落规模，同时人类的聚居拥有一定的自相似性:任何小聚居地日放大，便和整体十分相似，当中还有更小的聚居地。

城市规模越大，这样的城市出现概率越小

财富分布

幂律分布可以用来描述财富规模和频率之间的关系，即财富越大的人越少，财富越小的人越多。这种分布反映了社会中的不平等现象，也被称为二八法则、马太效应等。

例如，根据《2021胡润全球富豪榜》，全球有2095位财富超过10亿美元的富豪，他们的总财富达到了95万亿美元。而根据《2021全球财富报告》，全球成年人口有52.8亿，他们的总财富达到了418.3万亿美元。

财富规模和频率之间呈现出一条直线的关系，在对数坐标系中，这就是幂律分布的特征。也就是说，财富规模每增加一倍，拥有这个财富规模的人数就减少一定的比例。

财富的幂律分布被称为马太效应

自媒体关注度

文章阅读数量或者视频观看数量也可以用幂律分布来描述，即阅读或观看次数越多的文章或视频越少，阅读或观看次数越少的文章或视频越多。这种分布反映了网络内容中的头部效应和长尾效应，即少数的热门内容占据了大部分的用户注意力，而大量的冷门内容只能吸引少数的用户兴趣。

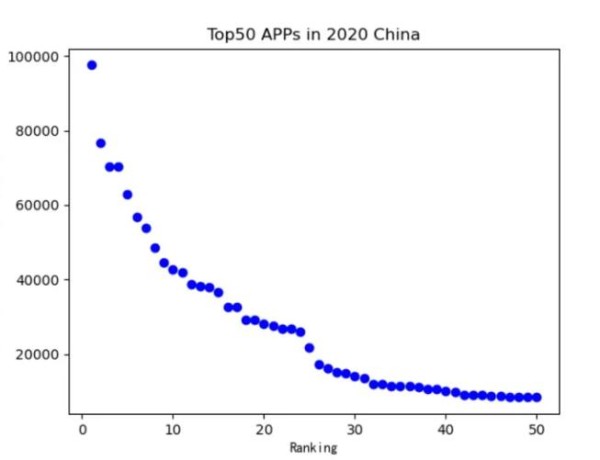文章、粉丝、用户数等等都服从幂律分布

幂律分布是一种重要的数学模型，它可以帮助我们理解自然界和社会现象中的许多规律和现象。通过学习幂律分布，我们可以发现世界上存在着许多标度不变的复杂系统，它们的行为受到正反馈和自组织临界等机制的影响。幂律分布也可以让我们认识到社会中的不平等和竞争，以及如何应对它们。幂律分布是一种有趣而有用的工具，它可以拓展我们的视野，启发我们的思维，增进我们的知识。

网址：幂律分布——自然界的另一种数学规律 https://m.mxgxt.com/news/view/1207922

相关内容

幂律分布
科学网—《意识、数学与自然规律： 段玉聪观点下的深度探索》
人生的幂定律
人生的幂定律。
一年级数学《找规律》案例与评析（精选13篇）
中国顶豪已呈现“幂律分布”现象
音乐旋律中的定量规律
吸毒贩毒的黄毅清为啥能越“渣”越火？因为有“幂律”分布作怪
移动社交网络幂律分布特征及亲属关系判别
美国财富不平等的幂律分布

随便看看